4.3.6.           Mathematische Berechnungen
4.3.6.1.             Wasserstrahlpumpe – Luftstrahldüse

In Abb. 13 ist das Schema einer Wasserstrahlpumpe dargestellt. Die hier erfolgte theoretische Untersuchung ist identisch mit der verwendeten Luftstrahldüse – bis auf einige Ausnahmen, auf die noch gesondert eingegangen wird. Die Pumpe besteht aus folgenden Hauptteilen:
Der Düse, durch die die Primärflüssigkeit (hier Wasser) aus einem Druckraum mit hohem Druck in einen Druckraum mit niedrigem Druck (Saugraum) gelangt, in dem der Primärstrahl mit der Sekundärflüssigkeit (Luft) in Berührung kommt – dem Mischraum, in dem sich das Primär- und das Sekundär-Medium mischen und dem Diffusor, in dem ein Teil der großen kinetischen Energie des eintretenden Wasser-Luft-Gemisches (bzw. Treib-, Falschluft) in statische Druckenergie umgesetzt und dadurch ein erhöhter Unterdruck in dem vorgeschalteten Misch- und Saugraum erzwungen wird.
Die Luftansaugung der Wasserstrahlpumpe wird aufgrund des mit hoher Geschwindigkeit ausströmenden Wasserstrahls durch den Injektionseffekt erreicht.
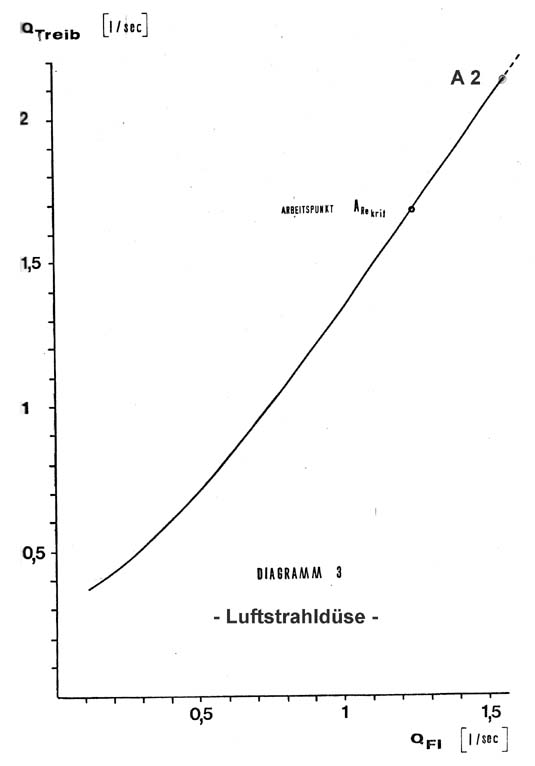
Der Durchsatz QFl des Sekundärmediums (Luft) ergibt sich als Funktion der Wassergeschwindigkeit (Treibmittelgeschwindigkeit b. d. Luftstrahldüse), des Druckverlaufs im Saug- und im Mischraum sowie den geometrischen Abmessungen der Düse und des Mischraumes. Dabei füllt der injizierte Falschluftstrom den Differenz-Querschnitt zwischen dem Mischraum und der Düse aus und strömt annähernd mit der Wassergeschwindigkeit v2. (Bei der Luftstrahldüse ist die injizierte Falschluftgeschwindigkeit nicht identisch mit der Treibmittelgeschwindigkeit, was noch aufgezeigt wird). Der wirkliche Luftdurchsatz VFl hängt selbstverständlich auch vom Widerstand bzw. Drosselung des Falschluftweges auf der Sekundärseite ab. (Siehe auch Abschnitt „4.3.5. Folgerungen“).

Mit dieser Gleichung 35) der Wasserstrahl-Luftpumpe kann der angesaugte Luftdurchsatz bei bekannten primärseitigen Drucken berechnet werden. Es ist auch möglich, die luftseitige Kennlinie zu erstellen, d. h. es kann gegen ein höheres Druckniveau gefördert werden (p3 › po). Die Verlustbeiwerte werden als Konstanten der Gleichung betrachtet.   4.3.6.2. Bestimmung der Verlustbeiwerte   Zunächst wird der Verlustbeiwert der Düse untersucht, welcher theoretisch Werte zwischen 0 und oo annehmen kann. Laut Literaturangabe (Versuch an Wasserstrahlpumpen) {3} liegt      Dü  -spiegelglatte Oberflächenausbildung Voraussetzung - bei Dü ~ n14 mit n1 = d2/d1 . Bei der von mir konstruierten Düse lässt sich diese Aussage nicht treffend vertreten. Um die Durchflüsse bzw. Drucke messtechnisch zu erfassen, wurde QFl  gegen QTreib gemessen. Siehe Tabelle 3 und Diagramm 3. Diese Funktion ist nur im oberen Bereich linear, so dass hier über einen weiten Bereich die Steigung konstant ist. Es lässt sich erkennen, dass der Falschluftanteil bis zu 43 % des gesamten Volumenstromes ausmacht – theoretisch möglich sind 50 %. Tabelle 3       -          Treibluft gegen Falschluft   QFl (l/sec)                  QTreib (l/sec)              QFl . 100 %                                                                                    Qges 0,122                         0,375                         24 % 0,155                         0,394                         28 % 0,408                         0,59                            41 % 0,62                           0,86                            42 % 0,833                         1,168                         42 % 1,114                         1,5                              43 % 1,33                           1,76                            43 %   Da sich das Manometer zur Messung von p1 weit vor der Düse befindet, gehen die Verluste dieser Zwischenstrecke als Erhöhung des Verlustbeiwertes ein.

 
4.3.6.3                     Folgerung und Diskussion
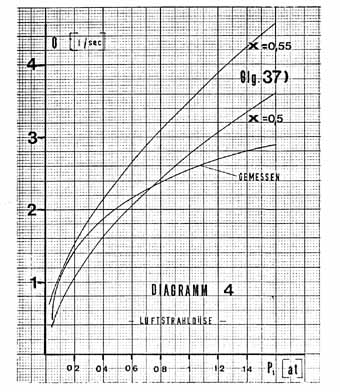
Im folgenden soll nun die abgeleitete Gleichung 35) der Wasserstrahl-Luftpumpe mit den festgelegten Verlustbeiwerten untersucht werden.
Für den Diffusordruckumsetzungsfaktor    (Glg. 25) ergibt sich

x                    =          0,0981

(Der Verlustbeiwert des Diffusors mach sich erst an der 4. Stelle von x bemerkbar.)

Diese Werte in Glg. 35) eingesetzt, ergeben Falschluftwerte, welche um ca. 300 % über den gemessenen liegen. Für p3 wird Außendruck mit 10.000 kp/m2 angenommen. Der Saugraumdruck po sowie p2 wird mit 50 kp/m3 Unterdruck belastet.

Diese zu hoch berechneten Falschluftwerte lassen den Schluss zu, dass die Falschluftströmungsgeschwindigkeit nicht identisch mit der Treibmittelstrahlgeschwindigkeit ist.

Dies ist folgendermaßen zu interpretieren:

1) Die Verlustbeiwerte können nicht als Konstanten angesehen werden.

2) Der Faktor x kann nicht als konstant angenommen werden, d. h. man kann die Geschwindigkeit der angesaugten Falschluft nicht als konstantes Verhältnis zur Treibmittelgeschwindigkeit ansehen, sondern dieses Verhältnis ändert sich in Abhängigkeit von den Volumenströmen.

Bei der Wasserstrahlpumpe wird die Falschluft im Trägermedium Wasser als eingeschlossene Gasblasen über den Querschnitt des Mischraumes verteilt und mit der Wasserstrahlgeschwindigkeit transportiert. (  Wasser >>  Luft). Das Treibmittel bei der Luftstrahldüse hat das gleiche spez. Gewicht wie die angesaugte Falschluft ( Treib ≈  Fl), so dass hier diese Diskrepanz zur Glg. 25) auftritt.